An interesting problem was asked on #Sqlhelp recently about adding very large numbers, in excess of 20 digits in SSAS tabular model. While most of us will find that bigint or decimal datatype is large enough for anything we can imagine storing; it is still an interesting problem. Mostly because as the volume of data increases we are bound to get to a point where even 20 digits might seem insufficient. Until say recently trillions were still considered rare which the case is no longer.
So how do we approach the problem?
Let’s assume for now that the numbers individually are in the very large number scale and we encounter the issue only when we add them. Let’s assume we create a table with a bigint datatype as shown below
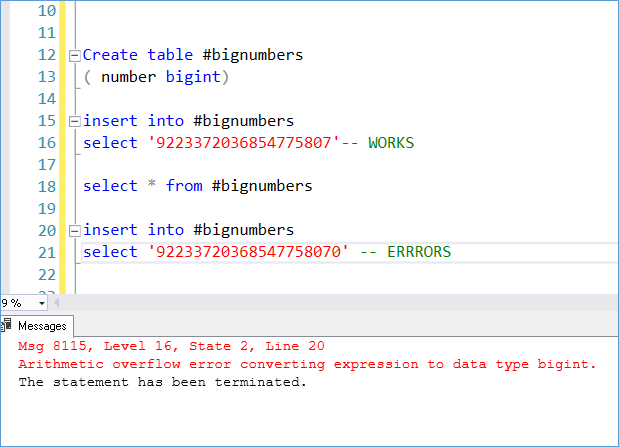
The solution here would be simply to change the datatype to decimal (38, 0)
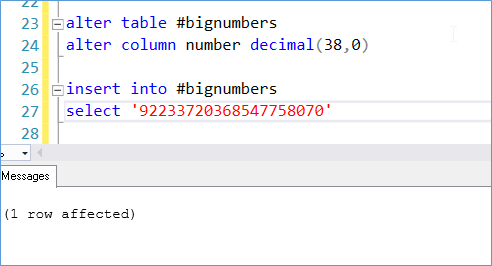
But what If we encounter numbers bigger than this?
No problem because we can store up to 38 digits into the decimal datatype
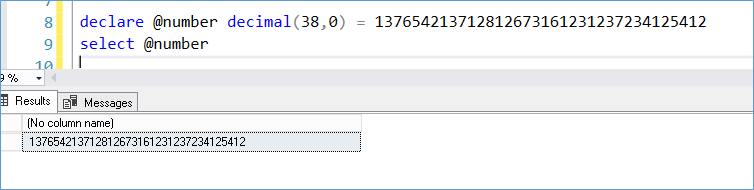
Let’s go for an even larger number 137654213712812673161231237234125412123132
Now even the decimal datatype is insufficient, do we have another datatype capable of storing even larger numbers?
Unfortunately not, so we need to implement some sort of work around. We could store the data into a varchar(200) data type so that the number is represented as its actual value however at this point we lose all ability to perform math operations on the underlying datatype.
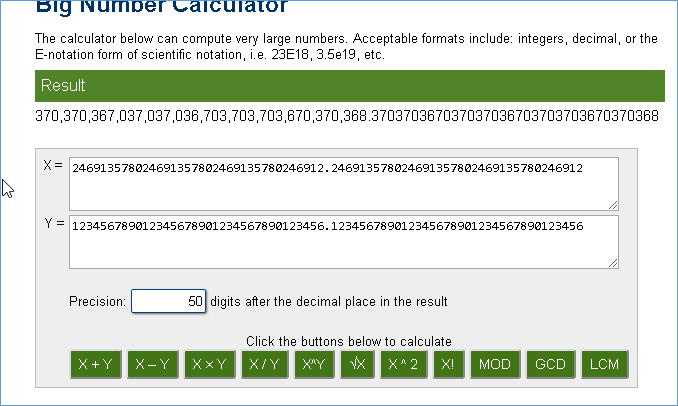
In this approach I have used the string datatype to break the number into smaller sets and then perform the operation on the smaller set first. Here is the result we are trying to verify.
First I have a table in which the numbers are being stored.
CREATE TABLE [dbo].[bignumbers] (
[id] [int] IDENTITY(1, 1) NOT NULL
,[number] [varchar](100) NULL
) ON [PRIMARY]
Then I Insert some random numbers into the table
INSERT INTO bignumbers
SELECT '123456789012345678901234567890123456.123456789012345678901234567890123456'
Finally I run the below script to generate the SUM of the above numbers. I have written the code in a bit of a hurry so please don’t judge me for not making it pretty. Also I am sure it could be rewritten to be a bit more efficient. But I haven’t tried that yet maybe in another post.
The below code has been tested for up to decimal (73, 36), Please feel free to share your thought and let me know if you find an error.
DROP TABLE #results
DECLARE @SigDigits INT = (
SELECT MAX(LEN(CAST(SUBSTRING(number, CHARINDEX('.', number) + 1, 100) AS DECIMAL(38, 0))))
FROM bignumbers
)
DECLARE @DVal AS VARCHAR(100)
SELECT @DVal = SUM(CAST(SUBSTRING(number, CHARINDEX('.', number) + 1, 100) + REPLICATE('0', @SigDigits - LEN(SUBSTRING(number, CHARINDEX('.', number) + 1, 100))) AS DECIMAL(38, 0)))
FROM bignumbers
DECLARE @Carryover INT = 0
IF LEN(@DVal) > @SigDigits
BEGIN
SET @Carryover = left(@DVal, len(@DVal) - @SigDigits)
SET @DVal = RIGHT(@DVal, @SigDigits)
END
DECLARE @Reaval AS DECIMAL(38, 0)
DECLARE @Realprecision AS INT
SELECT 'Little' = sum(cast(CASE
WHEN LEN(substring(number, 1, charindex('.', number) - 1)) >= 37
THEN RIGHT(substring(number, 1, charindex('.', number) - 1), 37)
ELSE substring(number, 1, charindex('.', number) - 1)
END AS DECIMAL(38, 0))) + @Carryover
,@DVal AS Decimals
INTO #results
FROM bignumbers
SELECT cast(Little AS VARCHAR(38)) + '.' + cast(Decimals AS VARCHAR(38)) AS Final
FROM #results
Proof is in the pudding.
Please Consider Subscribing